because of this, "sin 2" could be the sine of the real number 2, OR the sine of an angle of 2 radians
You can interpret trigonometric functions of real numbers geometrically by using a unit circle:
The radius of the circle is 1, with the center at the origin of a rectangular coordinate plane.
We will use the variable t as the radian measure of the angle theta or as the lenght of the black-highlighted circular arc on the circle above.
Definition of the Trigonometric Functions in Terms of a Unit Circle:
sin t = y cos t = x tan t = y/x
csc t = 1/y sec t = 1/x cot t = x/y
Finding values of trigonometric functions:
If point P is at the coordinates (-3/5, -4/5), find the values of the trigonometric functions at t (theta).
Use the definition of trigonometric functions in terms of a unit circle to get your answers.....
sin t = y = -4/5 cos t = x = -3/5 tan t = y/x = (-4/5)/(-3/5) = 4/3
csc t = 1/y = 1/(-4/5) sec t = 1/x = 1/(-3/5) cot t = x/y = (-3/5)/(-4/5) = 3/4
Theorem on Repeated Function Values for sine and cosine: If n is any integer, then
sin (t + 2 n) = sin t and cos (t = 2
n) = sin t and cos (t = 2 n) = cos t
n) = cos t
Graphing Functions
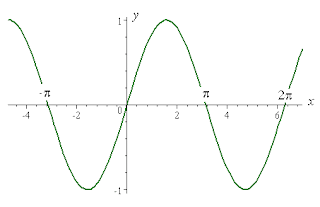
Graph of y = sin x:
y = cos x:
The part of the graph of the sine or cosine function where x is greater or equal to 0 and less than or equal to 2 is called one cycle. These cycles are sometimes refered to as a sine wave or a cosine wave.
is called one cycle. These cycles are sometimes refered to as a sine wave or a cosine wave.
y = tan x:
y = csc x:
y = sec x:
y = cot x:
Formulas for Negatives:
Theorem on Even and Odd Trigonometric Functions:
1. The cosine and secant functions are even.
2. The sine, tangent, cosecant, and cotangent functions are odd.
That's All Folks!
-Henry Burg









No comments:
Post a Comment