Section 9.6

9.6: The Algebra Arithmetic of Matrices

In this section, we will discuss the properties of matrices, and what it takes to add, subtract, and multiply them. There are certain conditions for these matrix operations that you must remember.

ADDITION OF MATRICES

First, let's talk about the addition of two or more matrices.

Note: You may only add two ore more matrices together if they have the same dimensions. 

In order to add two or more matrices, you must add the corresponding elements of each matrix together.

For example, if

   

 

SUBTRACTION OF MATRICES

The subtraction of matrices is similar to the addition of matrices, except that unlike addition, it is NOT commutative. The two or more matrices still must have the same dimensions. In order to subtract two or more matrices, you must subtract the corresponding elements of each matrix.

For example, if

MULTIPLICATION OF MATRICES

There are two forms of multiplication of matrices. The first is multiplying a matrix by a real number. Like the addition and subtraction of matrices, this operation is quite simple and just involves distributing the number to each element of the matrix. It will look like this:

The second form of the multiplication of matrices is a bit more confusing. Although the matrices can have different dimensions, there are still strict conditions that these dimensions must follow.

The best way to figure out if A) the matrices are multipliable and B) what the dimensions of the resulting matrix will be is to write out the dimensions side-by-side like so:

As the graphic shows, the inside numbers MUST match, or else the matrices cannot be multiplied. To find the dimensions of the resulting matrix, use the outside numbers - the number of rows of the first matrix by the number of columns of the second matrix.

Now the process of multiplying the matrices is quite hard to explain in a blog post. The best way to start is two write out your brackets for the resulting matrix and go element by element slowly. To multiply, use the rows of the first matrix and the columns of the second.

If you are given two matrices:

,

Then their dimensions are 2x3 and 3x2. They will multiply, and the resulting matrix will be 2x2.

It will look like this:

Okay, since I did a pretty horrible job explaining that, here are some links that'll hopefully help you out.

Multiplying Matrices Video 1

Multiplying Matrices Video 2

Multiplying Matrices Video 3

Wikipedia (Wilhelm approves)

mathsisfun.com - Multiplying Matrices

By Olivia Darany

9.5 - Systems of Linear Equations in More Than Two Variables A.K.A. Matrices

A Matrix is a seires of numbers within a set of brackets. These numbers are the coefficients of of each different variable called the Coefficient Matrix, and the last row is usually what the equation equals, called the Augmented Coefficient Matrix or Augmented Matrix. The last row of an augmented matrix is seprated by a line.

 Coefficient Matrix

Augmented Matrix

Definition of a Matrix

A matrix's size is determined by m and n. m is the number of rows the matrix has, and n is the number of comlumns a matrix has. 

Theorem on Matrix Row Transformations

Given a matrix of a system of linear equations, a matrix of an equivalent system results if:

1.) two rows are interchanged

2.) a row is multiplied or divided by a nonzero constant

3.) a constant multiple of one row is added to another row

Echelon Form of a Matrix

1.) The first nonzero number in each row, reading from left to right is 1.

2.) The column containing the first nonzero in any row is to the left of the column containing the first nonzero number in the row below.

3.) Rows consisting entirely of zeros may appear at the bottom of the matrix.

Guidlines for Finding the Echelon Form of a Matrix

1.) Locate the FIRST column that contains nonzero elements, and apply simple row transformations to get the number 1 into the first row of that column

2.) Apply simple row transormations of the type kR1+Rj-->Rj for j>1 to get 0 underneath the number 1 obtained in guidline 1 ineach of the remaining rows.

3.) Now, DISREGARD THE FIRST ROW. Locate the next column that contains nonzero elements, and apply simple row transformations to get the number 1 into the SECOND row of that column.

4.) Apply simple row transformations of the type kR1+Rj-->Rj for j>2 to get 0 underneath the number 1 obtained in guidline 3 in each of the remaining rows.

5.) Now, DISREGARD THE SECOND ROW. Locate the ext column that contains nonzero elements, and repeat. 

6.) Continue the process until the echelon form is reached.

Reduced Echelon Form

Reduced Echelon Form is the same as Echelon form, except in the non augmented part of the matrix there will only be 1's and 0's.

Matrices are AWESOME!!!

Austin

8.3 Vectors

Vectors have both magnitude and velocity.
This is unlike scalar quantities, who only have one value, such as time, mass, or length.
Those kinds of quantities are much less interesting.

Furthermore, if considering one space on the x-axis "i" and one space on the y-axis to be "j", then the length of OA=2i+3j. The direction of a vector can be expressed as an angle.

When adding vectors, you add from the tail of the first to the head of the second. A third vector is created from adding two vectors of different length and direction.


The same rule applies to when adding multiple vectors.

When the vectors share the same origin, the resulting vector is the diagonal of the parallelogram formed by the original vectors.
When adding vectors A and B to equal R, R's coordinates are (a1+b1,a2+b2).

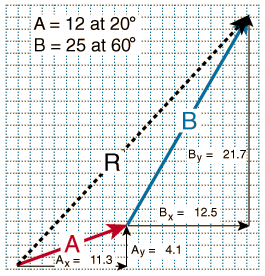
Example of Vector Components Finding the components of vectors for vector addition involves forming a right triangle from each vector and using the standard triangle trigonometry. The vector sum can be found by combining these components and converting to polar form.	Index Vector concepts
HyperPhysics***** Mechanics R Nave	Go Back

For vector R, where a=ix and b=jy, and magnitude of R=||R||, then .
In the case of the above R, .
                                          
                                          

When subtracting vector B from vector A, multiply B by -1 and then add the resulting vector to A.

Stay classy.
-Noah

9.3 System of Inequalties

9.3 System of Inequalities


Ex:

1. y^2< x+4
2. 3x-4y >12
3. x^2+y^2 >16

Terms:

• solution- an ordered pair that makes the statement true
• solve- find all real solutions
• graph- all the points (x,y) on the xy plane
• equivalent- the same solution
• test point- random point to see where there is a solution                                                            

Guidelines for Sketching Graph of Inequality in x and y

1. replace inequality sign with equal sign
2. graph the resulting equation
3. use dashes if < or >... otherwise use normal line
4. use test point to see where to solutions
5. shade solutions
6. if more than one inequality, use 1-5 for all... all shaded area is the final solution (works in all equations)

The whole chapter is pretty much that easy 

For a blob of pictures http://tutorpartner.blogspot.com/2011/01/systems-of-linear-inequalities-and.html

and just an overall better study guide http://www.purplemath.com/modules/ineqgrph.htm

-Pete

Systems of Equations

Hi Everyone! Today in class we reviewed how to solve systems of equations.

A system of equations is two or more equations using the same variables and solutions to systems of equations are values for the variables that make all of the equations true.

There are three ways to solve systems of equations; substitution, elimination, and graphing.

Substitution:
Here are the book's steps for substitution
1. Solve one of the equations for a variable x in terms of the other variable y.
2. Plug the expression for x into the other equation.  Now this equation will only have y's in it.
3. Solve the equation for y.
4. Plug the y value into the original equation from step 1 and solve for x.

Here's a sample problem using Substitution.
x+y = 6
x+2y = 3

Start by solving the first equation for x:
         x = 6-y
Then substitute that expression for x in the second equation and solve for y:
         (6-y)+2y = 3
         6+y = 3
         y = -3
Plug -3 into one of the original equations and solve for x:
        x+(-3) = 6
        x = 9
So, x = 9 and y = -3 are the solutions!

Elimination:
We didn't need to use elimination in our homework, but here's a sample problem anyway.

2x + y = 9
3x – y = 16

Start by 'adding' the equations because the y's will cancel out:
2x + y = 9
3x – y = 165x = 25
x = 5
Then plug x into one of the original equations:
2(5) + y = 9
10 + y = 9
y = –1

The solutions to this system are x = 5 and y = -1

Graphing:
To solve by graphing, you graph both of the equations and where they intersect are the solutions.

2x – 3y = –2
4x + y = 24

First solve each equation for y:
2x – 3y = –2
2x + 2 = 3yy = (2/3)x + (2/3)

4x + y = 24
y = –4x + 24

Next, graph the equations:



From this graph you can see that the intersect is (5,4).
So, the solutions to this system are x = 5 and y = 4.

That's basically it for solving systems of equations.
        -Olivia R

Section 8.2 - Law of Cosines

Hi, this section was about the law of cosines. Yay, fun.

Law of Cosines

The book says...
      Law of Cosines: the square of the length of any side of a triangle equals the sum of the squares of the lengths of the other two sides minus twice the product of the length of the other two sides and the cosine of the angle between them.

That pretty much means that...
       in any triangle ABC with sides a, b, and c...

     you generally use Law of Cosines with SAS or SSS

So, let's prove it.

We are given the oblique triangle ABC, 

To find the length of c, we use the distance formula.

Now, let's look at an example.

Area of a Triangle

To find the area of a triangle, you can use...

Unless you have a right triangle, getting the base and height can be a bit difficult so we were given three new equations for the area of a triangle. 

       Area of a triangle: is 1/2 the product of the lengths of any two sides of the triangle and the sine of the angle in between the two sides. 

We are given one more formula. Heron's formula, this is another way to find the area of a triangle

       Heron's formula: the area of a triangle with sides a, b, and c, is given by...

Yep, that was really fun. Hope it's helpful.

Carly

8.1 The Law of Sines

Hi! So this section is about the Law of Sines. Its good if you have a triangle thats oblique, or a triangle without a right angle, which is most triangles in the world.



So here we have our basic arbitrary triangle with sides a, b, and c and angles α, β, and γ. We have also drawn an altitude, h. From here, we can derive the Law of Sines.


sin α= h/b, so h= b sin α


AND


sin β= h/a, so h= a sin β


If we set the two equations equal to eachother, we get
b sin α= a sin β, or (sin α)/a= (sin β)/b


If we draw another altitude, we could also prove that (sin γ)/c is equal to these two.




So... in the end this is what we get:

If you want to use this formula, you need to know a minimum of three parts of the triangle. You can use it when you know these parts:

1. SSA - two sides and the angle opposite one of them

2. AAS/ASA - two angles and any side

To find SAS or SSS, we will have to use the Law of Cosines instead.

Theres also something important you have to keep in mind when solving with SSA. Sometimes, you solve for the sine of an angle, and you get some number between 0 and 1. There are 2 angles between 0 and 180 that have that sine, because sine functions are positive in the 1st and 2nd quadrants. This is called the ambiguous case. 

So how do you decide which angle is right? The important thing to remember is that if the measure of angle α (or β or γ) is greater than 90 degrees, than side a>b (or b>c or c>a.) If this is not the case, than angle α is acute.

That's pretty much all we covered in this chapter, so sorry the blog is so short! Bye!